Aktivitet

Digitale værktøjer i matematikundervisningen

Denne artikel sætter fokus på digitale værktøjer, der giver matematikundervisningen mange nye og gode muligheder for at understøtte udviklingen af elevernes matematiske kompetencer. 

 

Udviklingen inden for digitale værktøjer gør det vigtigt, at lærerne løbende genovervejer didaktik og mål i forhold til deres matematikundervisning.

Med digitale hjælpemidler kan eleverne hurtigt lave beregninger og konstruktioner. Det kan give dem indsigt i matematiske sammenhænge og flere muligheder for at arbejde analytisk og vurderende, eksempelvis ses ændringer løbende på en model, når eleverne ændrer på en variabel i en funktionsforskrift.

 

Valg af grundprogrammer

Der findes mange muligheder for at bruge programmer på nettet og på telefonen. Fagene bruger forskellige programmer og fagportaler, og eleverne kan i nogle tilfælde blive forvirrede over:

  • Hvilket program skal vi bruge nu?
  • Hvor skal vi logge på?
  • Skal vi bruge...eller...?
  • Hvor og hvordan gemte vi sidste gang? 
     

Derfor bør skolen/teamet have en strategi for, hvordan og hvilke programmer/hvilke digitale hjælpemidler, der bruges. Det anbefales at bruge få programmer, der tilsammen skal dække CAS, regneark og dynamisk geometri. Herunder gives et bud på, hvad tre forskellige typer af programmer kan bidrage med til matematikundervisningen.

CAS

  • Udregninger: Store og komplicerede udregninger løses let.
  • Ligninger: Ligningsløsning bliver hurtigt og problemfrit.

Regneark

  • Databehandling: Det bliver nemt og overskueligt at behandle store mængder af data, eksempelvis statistik.
  • Visualisering af data, for eksempel diagrammer.
  • Dynamisk modellering af udvikling, for eksempel budgetter.
  • Målsøgning: Regnearket kan finde resultatet ud fra kendte sammenhænge.

Geometriprogram

  • Visuel repræsentation: Det bliver let at se ændringer i eksempelvis statistik, funktioner og konstruktioner i både 2D og 3D.
  • Undersøgelse: Undersøge og opdage geometriske sammenhænge.
  • Animationer: Programmering og visualisering af matematik

Alle tre typer af programmer kan støtte eleverne i at arbejde undersøgende, analytisk og vurderende i forhold til både det skriftlige og mundtlige arbejde i matematikundervisningen.

 

Eksempler på anvendelse af digitale hjælpemidler

Herunder gennemgås konkrete eksempler på anvendelsen af CAS-værktøj, geometriprogram samt regneark.

 

CAS
Digitale værktøjer kan anvendes i undervisningen og bidrage til at flytte elevernes læring fra fokus på specifikke algoritmer til udvikling af generel matematisk forståelse. Det kan for eksempel ske i arbejdet med ligningsløsning. CAS-værktøjet giver mulighed for, at løsning af ligninger bliver til en induktiv problembehandling frem for en reproduktion ved hjælp af en deduktiv fremgangsmåde.

Eksempel på ligningsløsning med CAS
Find 3 på hinanden følgende tal, som giver 39. Opsættes via ræsonnement til denne model:

  • x+(x+1)+(x+2)=39
  • ⇕ Ligningen løses for x vha. CAS-værktøjet
  • x=12

De tre tal er derfor 12, 13 og 14.

I ovenstående eksempel kan eleverne få problembehandlings-, ræsonnements- og modelleringskompetencen i spil.

 

Geometri
I et geometriprogram kan eleverne undersøge geometriske sammenhænge og løbende følge med i ændringer, da programmet viser udviklingen dynamisk.

Eksempel på undersøgelse i geometriprogram
Undersøg, om en median deler en trekant i 2 lige store dele.

  • Tegn en vilkårlig trekant.
  • Indsæt en median.
  • Mål arealet af de 2 nye trekanter.
  • Flyt på punkter, så sidelængder og vinkler ændres.
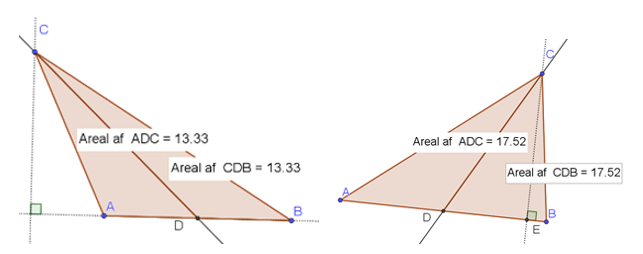
© Børne- og Undervisningsministeriet

 

Hvad kan konkluderes?
Når eleverne har opdaget sammenhængen, kan de forsøge at bevise/argumentere via algebra/ræsonnement. I dette og flere tilfælde kan digitale værktøjer være en øjenåbner og skabe en nysgerrighed. Hvis eleverne forfølger deres nysgerrighed, vil det være en gevinst for eleverne og for undervisningen.

 

 

Regneark
Herunder gennemgås et eksempel på, hvordan der kan arbejdes med undersøgelse i regneark.

Eksempel på undersøgelse i regneark
Eleverne skal bygge et kasseformet akvarie. Længden skal være 1,6 gange længere end bredden. Højden skal være 2 gange længere end bredden. Undersøg hvor meget glas, der skal bruges til et akvarium, der skal indeholde 1200 liter.

I et regneark kan eleverne indsætte følgende:

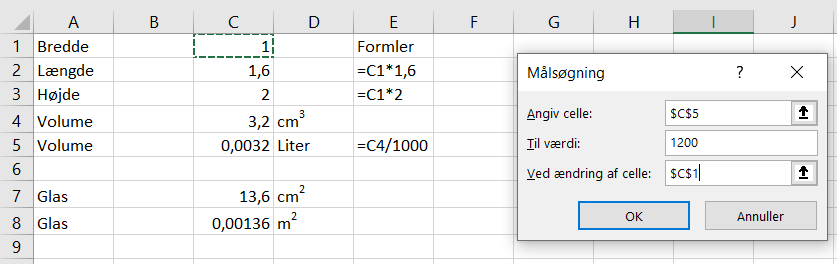
© Børne- og Undervisningsministeriet

 

Ved hjælp af en målsøgning (Data à What if-analyse à Målsøgning), kan eleverne nu se, at der skal bruges ca. 7 m2 glas til et akvarium med 1200 liter vand.

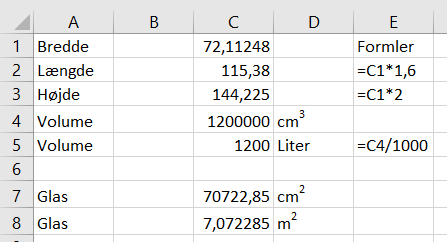
© Børne- og Undervisningsministeriet

 

Eksemplet kan også løses som ligningsløsning i et CAS-program eller i GeoGebras 3D-vindue, hvor længde og højde er afhængige af bredden via en variabel. Elever med gode hjælpemiddelkompetencer kan dermed anvende det hjælpemiddel, som giver mest mening for dem.

 

 

 

 

Styrker ved anvendelse af digitale værktøjer i matematikundervisningen

 

Hvornår hjælper digitale værktøjer den fagligt udfordrede matematikelev? Hvad giver det eleven?

Hvornår hjælper digitale værktøjer den dygtige matematikelev? Hvad giver det eleven?

 

  • Bygger bro over matematikhuller (jf. Matematik nr. 1, 2010).
  • Giver mulighed for flere repræsentationer.
  • Giver mulighed for visualisering af opgaver.
  • Udregninger på computeren kan nemmere følges og rettes end på lommeregneren.
  • Tekstbehandling giver mulighed for at samle CAS/regneark/geometri/skærmbilleder og kan give eleven et overblik over løsningen.

 

  • Løfter problemløsning op på et højere taksonomisk niveau.
  • Giver mulighed for at opdage noget, som eleven kan undersøge videre.
  • Dynamiske modeller kan nemt og hurtigt give indsigt i sammenhænge, fordi lignende eksempler kan ændres og påvirkes.

 

Det er vigtigt at være opmærksom på, at elever også kan have udfordringer med at anvende de digitale værktøjer. Derfor er det vigtigt at give eleverne ekstra opmærksomhed, så de ikke mister motivationen. Den ekstra opmærksomhed skal gå både på det matematik-faglige og det it-faglige.

For alle elever kan det være en fordel, at læreren benytter digitale værktøjer til formidling af matematikken, fordi formidlingen kan visualiseres ved hjælp af disse. Det gælder eksempelvis:

  • 3Dtegninger
  • Luftfoto af skolen
  • Dynamiske repræsentationer (Jf. Læreren smitter! Matematik nr. 3, 2019)
    • Regneark
    • Funktioner
    • Geometriske figurer

 

Inspiration til fagteamet

Herunder er listet en række eksempler på spørgsmål, der kan diskuteres i faggruppen inden anvendelsen af digitale værktøjer i matematikundervisningen:

  • Hvornår og hvordan bruger elever/lærere computer i undervisningen?
  • Hvilke muligheder for læring får eleverne ved inddragelse af digitale værktøjer? Mister de noget?
  • Husker eleverne det lærte dårligere eller bedre, når de bruger digitale værktøjer?
  • Hvordan kan digitale værktøjer bidrage til udvikling af elevernes matematiske kompetencer?
  • Hvornår er ”Blackbox” ok?

Der kan også sættes fokus på, hvorvidt inddragelse af digitale hjælpemidler har ændret på de emner, der arbejdes med i matematik? I den forbindelse kan spørgsmål som disse diskuteres i temaet:

  • Hvorfor regne top- og nulpunkter, når eleverne kan få vist skæringspunkter grafisk?
  • Hvorfor beregne areal af ikkeregulære figurer, når eleverne kan tegne dem forholdsvis hurtigt i et geometriprogram og få programmet til at vise areal/omkreds?
  • Hvorfor lære gangetabeller eller andre færdigheder, når eleverne har et digitalt hjælpemiddel?

 

Gode råd

Herunder er samlet en række gode råd i forhold til arbejdet med og anvendelsen af digitale værktøjer i matematikundervisningen:

  • Vær vedholdende, selvom det driller i starten, og hjælp hinanden undervejs med at dele erfaringer og viden.
  • Skab i fagteamet en fælles forståelse for, hvorfor og hvornår eleverne skal bruge digitale hjælpemidler, samt hvilke programmer eleverne skal anvende og hvordan.
  • Diskuter med eleverne, hvornår det er en fordel at anvende digitale hjælpemidler, og hvilke begrænsninger der er i de digitale hjælpemidler.
  • Sørg så vidt muligt for, at alle eleverne har adgang til samme type digital-enhed, eksempelvis Chromebooks/bærbar computer/iPad.
  • Undervis eleverne i de programmer, der bruges.
  • Hav en it-vejleder, som hurtig kan hjælpe elever med it-problemer.
  • Forsøg at skabe et formaliseret samarbejde mellem indskoling, mellemtrin og udskoling. Det er en god ide, hvis eleverne i udskolingen kan drage fordel af det, de har lært i indskolingen, og det anbefales, at der er en rød tråd i elevernes skriftlige arbejde.
  • Tag, hvis det er muligt, på kursus i de programmer, som skolen bruger. Det er en fordel, hvis alle lærere deltager i sådanne kurser.
  • Vent med at bruge en færdig app, eksempelvis WordMats trekantsløser og statistikark, til eleverne har forståelse for begreber og opbygning.

 

Inspiration

Læs mere om it og medier i matematikundervisningen på side 111 i faghæftet for matematik.
Faghæftet findes her: Læseplan og vejledning

 

Kreditering

Artiklen er udarbejdet af Morten Graae, Kim Lorentzen, Anders Nielsen og Helle Fjord, der alle er matematiklærere på Bjergsnæs Efterskole.

Siden er opdateret af emu-redaktionen
Rettigheder:

Tekstindholdet på denne side må bruges under følgende Creative Commons-licens - CC/BY/NC/SA Kreditering/Ikke kommerciel/Deling på samme vilkår. Creative Commons-licensen gælder kun for denne side, ikke for sider, der måtte henvises til fra denne side.
Billeder, videoer, podcasts og andre medier og filer på siden er underlagt almindelig ophavsret og kan ikke anvendes under samme Creative Commons-licens som sidens tekstindhold.